The Measurement Problem in Quantum Mechanics
Measurement is probably the key concept in all of Physics, but in Quantum Mechanics it is a nebulous process that is still surrounded by mistery and contraddictions. Does that mean that our modern understanding of the world sits on wobbly foundations?
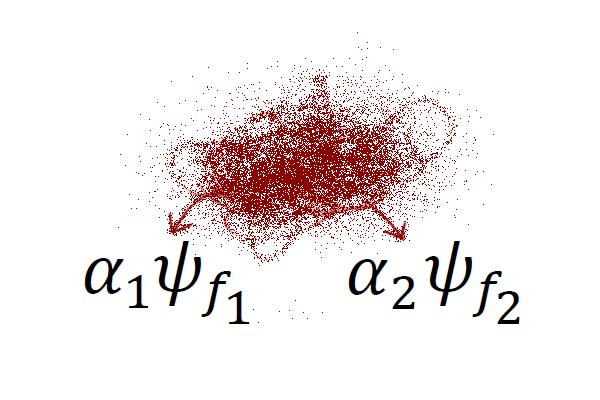
This work was written in collaboration with Prof. Canio Noce and published on Science and Philosophy 7 (1):41-58. You can read it on their website. If you have any question, don't hesitate to contact me at alessioferraioli@hotmail.it.
Abstract
In this paper, we discuss the importance of measurement in quantum mechanics and the so-called measurement problem. Any quantum system can be described as a linear combination of eigenstates of an operator representing a physical quantity; this means that the system can be in a superposition of states that corresponds to different eigenvalues, i.e., different physical outcomes, each one incompatible with the others. The measurement process converts a state of superposition (not macroscopically defined) in a well-defined state. We show that, if we describe the measurement by the standard laws of quantum mechanics, the system would preserve its state of superposition even on a macroscopic scale. Since this is not the case, we assume that a measurement does not obey to standard quantum mechanics, but to a new set of laws that form a “quantum measurement theory”.
Keywords
measurement theory; quantum mechanics; reduction postulate, quantum superposition
Full Article
Read the full article here.